Glazer notation for Octahedral Tilting in Perovskites

This tutorial explains how Glazer notation is used to identify Perovskites of different symmetries based on their atomic positioning.

What are Perovskites?

Perovskites are structures that take the form ABX$_3$ structure (E.g.- SrVO$_3$, CaTiO$_3$, CsSnI$_3$). The B cation has 6 fold coordination, surrounded by an octahedron of corner sharing anions. The A cation has 12 fold coordination surrounded by 12 anions. Most transition metallic ions are perovskite compounds. Some interesting properties of Perovskites include Ferroelectricity, colossal magnetoresistance, High T superconductivity etc.

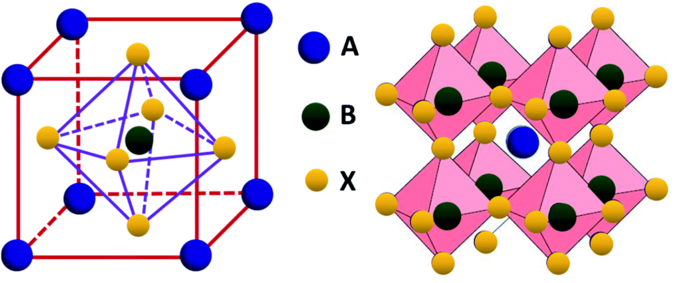
^{Image source: Yi et al.1} 

Octahedral tilting

Goldschmidt’s Tolerance Factor given from the following equation predicts the stability of perovskites.

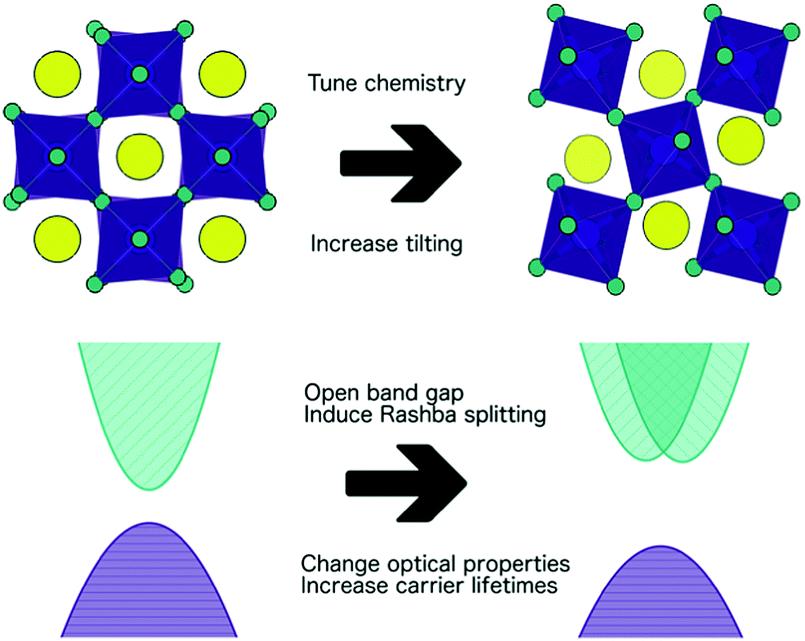
\[t=\frac{r_{\mathrm{A}}+r_{\mathrm{X}}}{\sqrt{2\left(r_{\mathrm{B}}+r_{\mathrm{X}}\right)}}\]

where, r$_A$, r$_B$ and r$_X$ are the ionic radii of the ions. t = 1 is a perfect cubic perovskite. Tilting occurs at lower t values where the A cation is small. Based on the relative sizes of the ions, defects, temperature effects the locations of the ions are shifted resulting in a tilting of the octahedral. E.g.- In CaTiO$_3$ octahedral tilting distortion lowers the coordination number of the A-site cation Ca$^{2+}$ from 12 to 8. This affects the system’s physical, magnetic, electric properties.

The following figure displays octahedral tilting and its effects².

Notation

\[a^0b^+c^-\]

• The sequence of the symbols corresponds to the crystallographic axes i.e. first symbol = tilt along a [100] etc.
• Identical characters indicate the same amplitude of tilt.
• The superscript indicates zero-tilt (0), in-phase-tilt (+) or anti-phase-tilt (-) of subsequent layers of octahedra.
• There exists 15 tilt systems for perovskites. The following is an example.

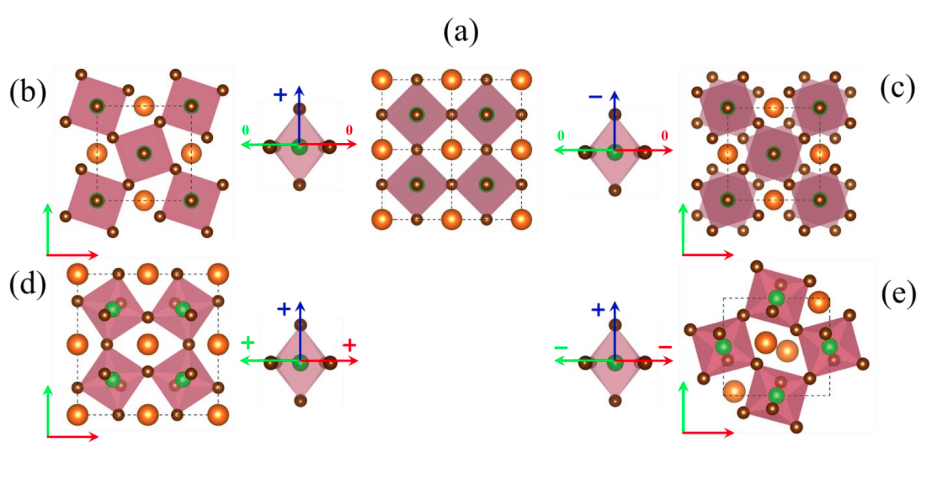
Structure	Glazer notation
a	a$^0$a$^0$a$^0$ (cubic)
b	a$^0$a$^0$c$^+$ (tetragonal)
c	a$^0$a$^0$c$^-$ (tetragonal)
d	a$^+$a$^+$a$^+$ (cubic)
e	a$^+$b$^-$b$^-$ (orthorhombic)

Table 1: The Glazer notations for the halide perovskite structures in the previous figure.

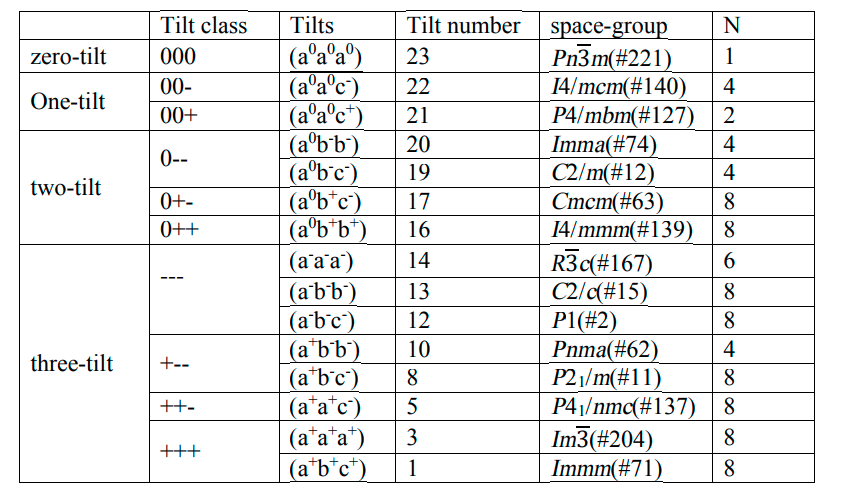
The following table summarizes the different types of tilting possible for different space groups³.

References

1. Yi, Z., Ladi, N., Shai, X., Li, H., Shen, Y., & Wang, M. (2019). Will organic–inorganic hybrid halide lead perovskites be eliminated from optoelectronic applications?Nanoscale Adv., 1, 1276-1289. ↩

2. Butler, K. (2018). The chemical forces underlying octahedral tilting in halide perovskitesJ. Mater. Chem. C, 6, 12045-12051. ↩

3. Shojaei, F. & Yin, W.-J. Stability trend of tilted perovskites. arXiv:1803.05604 [cond-mat] (2018). ↩

Sign up to get updates on my latest blog posts!

Thank you!

You have successfully joined my subscriber list.